阿部技術士・労働安全コンサルタント事務所は、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。
TEL. 088-694-3482
〒771-1330 徳島県板野郡上板町西分字橋北16番地2
技術情報メモ42Technical information
42)材料力学(はりの曲げ)
技術情報メモ38では材料力学(力学の基礎知識)、メモ39では材料力学(質量と力)、メモ40では材料力学(応力とひずみ)、メモ41では材料力学(軸のねじり)について紹介しました。ここでは材料力学(はりの曲げ)について紹介します。技術には危険がつきものです。このため、危険源を特定し、可能な限りリスクを減らすことによって、その技術の恩恵を受けることが可能となります。
例えば、自動車の登場は蒸気自動車が1769年、ガソリン自動車が1870年(内燃機関によるものでは1885年にそれぞれ発明したダイムラーとベンツによるものが最初)とされています。航空機は1903年にライト兄弟により初飛行が行われました。また、原子力発電は1951年にアメリカで初めて行われました。原子力発電については世界中で存続の是非が問われていますが、自動車と航空機については無くてはならないものになっています。それ故、今日まで、安全性向上のための技術開発等、不断の努力が続けられているのです。
機械工学はこれらの技術開発・改良に欠くことのできない学問です。特に、材料力学は機械や構造物が安全に運用されるための基礎となる学問です。材料力学の知識なしに設計された機械や構造物は危険源の塊かも知れません。
ここでは、真直ばりの応力について紹介します。
「はり」とはどのようなものでしょうか?JSMEテキストシリーズ「材料力学」では次のように記載されています。
図1のように、「細長い棒に横方向から棒の軸を含む平面内の曲げを引き起こすような横荷重を受けるとき、
このような棒をはり(beam)と呼ぶ。」
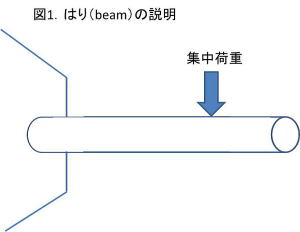
図1.はり(beam)
一端を壁に固定された片持ちはりに集中荷重が作用した場合を示しています。
図2-1、2-2は「はり」が曲げモーメントだけを受け、せん断力を受けない、単純曲げの状態を示したものです。
「はり」の断面が 左右対称で、対称軸と軸線を含む面内で、「はり」に曲げモーメントが作用した場合、「はり」は曲げモーメントの作用面内で曲げられます。このとき、「はり」の各部は垂直及び水平方向に移動(変位)します。
材料力学ではこの変位を軸線の変位で代表させています。この変位は実際の変位とは異なりますが、その違いは微小であるため無視できるとされています。
そして、「曲げられた「はり」の断面は平面を保ち、軸線に直交すると仮定できる」とされています。
以下では、これらの前提条件を考慮して求められた「はり」の曲げ応力について説明します。なお、引張と圧縮に対する縦弾性係数は等しいとしています。
図2-1のNN1は曲げの前後で伸縮しません。この部分を含む縦軸面を中立面、中立面と横断面の交線NN(図2-2)を中立軸といいます。点OはABとCDの延長線上の交点で、曲げの中心になります。その曲率半径ONをρとします。
KLのひずみεはKL/NN1=OK/ON(扇形の相似)であるから、
dX(1+ε)/dX=(ρ+y)/ρとなり、
ε=y/ρ が得られます。
従って、この部分に生ずる軸方向の垂直応力σは
σ=Eε=E(y/ρ)ーーー(1) となります。
図2-1に示したとおり、はりは曲げられることにより、中立軸の外側に引張応力(+σ)、内側に圧縮応力(-σ)が生じます。そして、これらの応力のことを曲げ応力とよびます。曲げ応力は図2-1の三角形(斜線)のように直線的に分布しています。中立面ではσ=0です。
次に、曲げ応力と曲げモーメントのつり合いを考えます。
曲げ応力σが中立軸のまわりにもつモーメントの総和は、曲げに対する抵抗となって断面の受ける曲げモーメントMとつり合います。
従って、
M=∫AσydA
これに、(1)式を代入すると、
M=(E/ρ)∫Ay2dA が得られます。
ここで、
∫Ay2dA=Iz とおくと、
1/ρ=M/EIz ---(2) と書き換えられます。
Izは断面Aの中立軸NNに関する断面二次モーメントといい、断面の形状寸法で決まる定数です。
式(1)と(2)より、
ρ=(M/Iz)y が得られます。
この式は曲げ応力と曲げモーメントの関係を表しています。
なお、断面二次モーメントIzははりの曲げ応力、曲げ剛性(EIz)、はりの変形を求めるのに重要な値なので、円形、長方形、中空円形など、代表的な形状については思い出せるようにしておくと便利です。
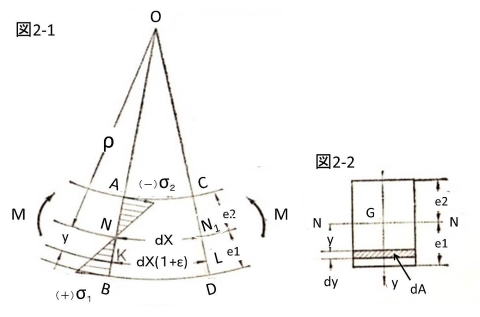
図2.はりの曲げ
単純曲げの状態を示したものです。
(出典/参考図書:
材料力学(黒木剛司郎))
バナースペース
阿部技術士・
労働安全コンサルタント事務所
〒771-1330
徳島県板野郡上板町西分字橋北
16番地2
TEL 088-694-3482
FAX 088-694-3482