阿部技術士・労働安全コンサルタント事務所は、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。
TEL. 088-694-3482
〒771-1330 徳島県板野郡上板町西分字橋北16番地2
技術情報メモ43Technical information
43)材料力学(はりのたわみ曲線)
技術情報メモ38では材料力学(力学の基礎知識)、メモ39では材料力学(質量と力)、メモ40では材料力学(応力とひずみ)、メモ41では材料力学(軸のねじり)、メモ42では材料力学(はりの曲げ)について紹介しました。ここでは材料力学(はりのたわみ曲線)について紹介します。技術には危険がつきものです。このため、危険源を特定し、可能な限りリスクを減らすことによって、その技術の恩恵を受けることが可能となります。
例えば、自動車の登場は蒸気自動車が1769年、ガソリン自動車が1870年(内燃機関によるものでは1885年にそれぞれ発明したダイムラーとベンツによるものが最初)とされています。航空機は1903年にライト兄弟により初飛行が行われました。また、原子力発電は1951年にアメリカで初めて行われました。原子力発電については世界中で存続の是非が問われていますが、自動車と航空機については無くてはならないものになっています。それ故、今日まで、安全性向上のための技術開発等、不断の努力が続けられているのです。
機械工学はこれらの技術開発・改良に欠くことのできない学問です。特に、材料力学は機械や構造物が安全に運用されるための基礎となる学問です。材料力学の知識なしに設計された機械や構造物は危険源の塊かも知れません。
ここでは、はりのたわみ曲線について紹介します。
「はり」とはどのようなものでしょうか?JSMEテキストシリーズ「材料力学」では次のように記載されています。
図1のように、「細長い棒に横方向から棒の軸を含む平面内の曲げを引き起こすような横荷重を受けるとき、
このような棒をはり(beam)と呼ぶ。」
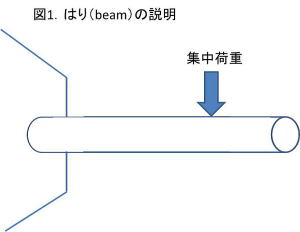
図1.はり(beam)
一端を壁に固定された片持ちはりに集中荷重が作用した場合を示しています。
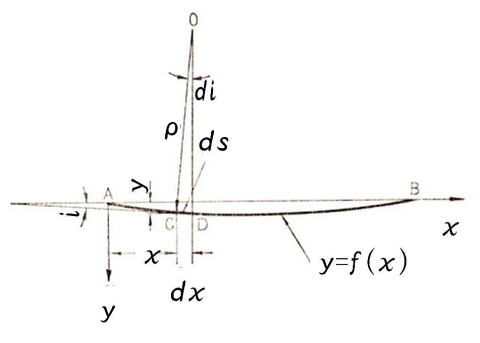
図2.はりの曲げ
単純曲げの軸線の状態を示したもの
です。
(出典/参考図書:
材料力学(黒木剛司郎))
図1に示すような「はり」に曲げモーメントが作用すると「はり」の軸線に曲がりが生じます。
そして、中立面の曲率(1/ρ)と曲げモーメントMとの間には次の関係が成立します。
1/ρ=M/EIz ---(1)
( Iz=∫Ay2dA )
次に、図2に示した近接する二点C、Dにおいて長さdsの曲線CDの曲率半径をρ、曲率中心をOとすれば、角CODはC点のたわみ角iの微小変化量diに等しくなり、次式が成立します。
1/ρ=-(di/ds) ---(2)
また、tan(i)=dy/dx であることから、式(2)は次のように展開されます。
1/ρ=-(di/ds)=-(di/dx)・(dx/ds)
=((-d2y/dx2)/(1+(dy/dx)2))×(1/(1+(dy/dx)2)1/2 )
=(-d2y/dx2)/(1+(dy/dx)2)3/2
弾性変形の範囲では、はりの全長に対し、たわみyは極めて小さく、たわみ角iも微小であるため、
上式において、(dy/dx)2は無視でき、1+(dy/dx)2≒1とみなせるので、次式が成立します。
1/ρ=-d2y/dx2 ---(3)
式(1)と(3)から、次式が得られます。
d2y/dx2=ー(M/EIz) ---(4)
式(4)は、たわみ曲線の式y=f(x)を求めるための微分方程式です。
ここでは、例として、図3に示した自由端に集中荷重を受ける片持ちばりの最大たわみ角と最大たわみを求めてみます。
EIz(d2y/dx2)=ーM=-(-Wx)=Wx
EIzy=(W/6)x3+c1x+c2
積分定数c1とc2は固定端x=ℓで、たわみ角dy/dx=0、たわみy=0の条件を満たすように定めると
次のようになります。
c1=-(W/2)ℓ2、
c2=-(W/3)ℓ3
dy/dx=(W/2EIz)(x2-ℓ2)
y=(W/6EIz)(x3-3ℓ2x+2ℓ3)ーーーたわみ曲線は三次曲線となります。
たわみ角とたわみの最大値は、自由端x=0で生じ、それぞれ、以下のとおりです。
最大たわみ角: (dy/dx)max=imax=-(Wℓ2/2EIz)
最大たわみ: ymax=Wℓ3/3EIz
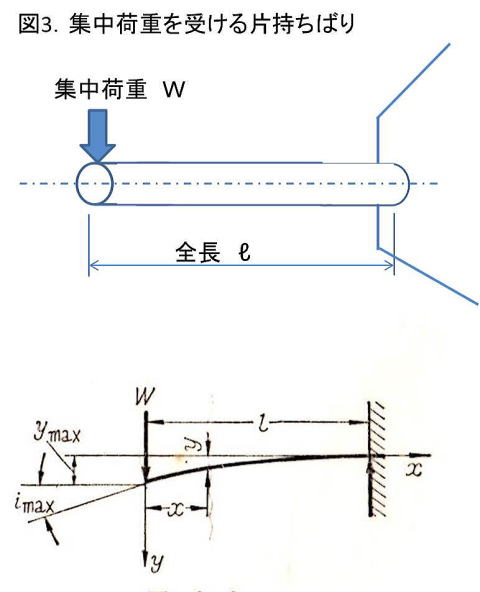
図3.片持ちはり
集中荷重を受ける片持ちばりの最大
たわみ角と最大た
わみ量を求めたも
のです。
バナースペース
阿部技術士・
労働安全コンサルタント事務所
〒771-1330
徳島県板野郡上板町西分字橋北
16番地2
TEL 088-694-3482
FAX 088-694-3482