阿部技術士・労働安全コンサルタント事務所は、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。
TEL. 088-694-3482
〒771-1330 徳島県板野郡上板町西分字橋北16番地2
技術情報メモ44Technical information
44)材料力学(ひずみエネルギーほか)
技術情報メモ38では材料力学(力学の基礎知識)、メモ39では材料力学(質量と力)、メモ40では材料力学(応力とひずみ)、メモ41では材料力学(軸のねじり)、メモ42では材料力学(はりの曲げ)、メモ43では材料力学(はりのたわみ曲線)について紹介しました。ここでは材料力学(ひずみエネルギーほか)について紹介します。技術には危険がつきものです。このため、危険源を特定し、可能な限りリスクを減らすことによって、その技術の恩恵を受けることが可能となります。
例えば、自動車の登場は蒸気自動車が1769年、ガソリン自動車が1870年(内燃機関によるものでは1885年にそれぞれ発明したダイムラーとベンツによるものが最初)とされています。航空機は1903年にライト兄弟により初飛行が行われました。また、原子力発電は1951年にアメリカで初めて行われました。原子力発電については世界中で存続の是非が問われていますが、自動車と航空機については無くてはならないものになっています。それ故、今日まで、安全性向上のための技術開発等、不断の努力が続けられているのです。
機械工学はこれらの技術開発・改良に欠くことのできない学問です。特に、材料力学は機械や構造物が安全に運用されるための基礎となる学問です。材料力学の知識なしに設計された機械や構造物は危険源の塊かも知れません。
ここでは、ひずみエネルギーほかについて紹介します。
エネルギーを計算することにより物体の変形を求めることができます。物体を変形させようとした場合、外部から物体に力を加えます。物体は変形することにより内部エネルギーが増加しますが、この変形に伴い増加した内部エネルギーのことを「ひずみエネルギー」とよんでいます。このひずみエネルギーを用いることにより物体の変形挙動を解明することが可能になります。
ここでは、最初に、「引張」、「せん断」、「曲げ」及び「ねじり」におけるひずみエネルギーを紹介します。
1)引張によるひずみエネルギー
図1の丸棒が、荷重Pにより、弾性変形し、δだけ伸びた場合、丸棒の保有するひずみエネルギーUは次式(1)で求められます。
U=∫dU=∫0δP1dδ1=Pδ/2 ---(1)
δとPの間には、フックの法則(σ=E・ε)が成立するので、縦弾性係数をEとすれば、次式が成立します。
δ=Pℓ/AE ---(2)
式(2)を式(1)に代入すると次式が得られます。
U=P2ℓ/2AE=AEδ2/2ℓ ---(3)
丸棒の断面積が変化するときは、次式となります。
U=∫dU=∫(P2/2AE)dX ---(4)
単位体積当たりのひずみエネルギーuは式(3)から求めます。
u=U/Aℓ=P2/2A2E=σ2/2E=Eε2/2=σε/2 ---(5)
(ここで、σ=P/A、ε=σ/E )
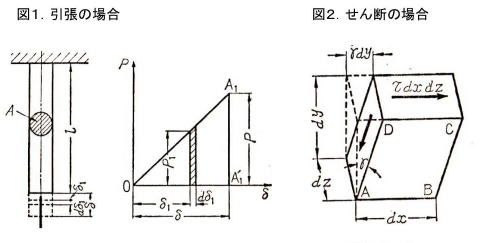
図1~2.ひずみ
エネルギ―
引張及びせん断の場合(出典/参考図書:
材料力学(黒木剛司郎))
2)せん断によるひずみエネルギー
図2の直方体がせん断応力を受け、弾性変形し、せん断ひずみγを生ずる場合のひずみエネルギーを求めます。
上面に外力(τdxdy)が作用し、下面に対し、(γdy)の変位が生じているので、外力による仕事は次式のようになります。
U=τdxdz・γdy ---(6)
式(6)は直方体が保有するひずみエネルギー量であり、単位体積当たりのひずみエネルギーuは次式で求められます。
u=τγ/2=Gγ2/2=τ2/2G ---(7)
(ここで、直方体の体積V=dxdydy、G:せん断弾性係数)
3)曲げによるひずみエネルギー
図3の曲げモーメントMを受け、弾性変形し、曲げ応力σを生ずる場合のひずみエネルギーを求めます。
断面の微小容積dV=dAdxに保有される引張又は圧縮応力によるひずみエネルギーは次式で求められます。
U=∫dU=∫(σ2/2E)dV=∫∫(σ2/2E)dAdx ---(8)
ここで、σ=(M/Iz)y を式(8)に代入すると次式が得られます。
U=∫∫(M2/2EIz2)y2dAdx=∫0ℓ(M2/2EIz2)dx・∫Ay2dA ーーー(9)
ここで、∫Ay2dA =Iz を式(9)に代入すると次式となります。
U=∫0ℓ(M2/2EIz)dx ---(10)
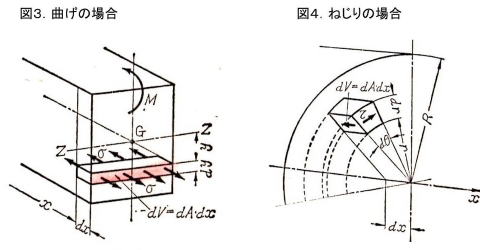
図3~4.ひずみ
エネルギー
曲げ及びねじりの場合(出典/参考図書:
材料力学(黒木剛司郎))
4)ねじりによるひずみエネルギー
図4の丸棒がねじりモーメントTを受け、弾性変形した場合に生ずるひずみエネルギーを求めます。
断面の微小容積dV=dAdxに保有されるせん断応力τによるひずみエネルギーは次式で求められます。
U=∫dU=∫(τ2/2G)dV=∫∫(τ2/2G)dAdx ---(11)
ここで、τ=(T/IP)r を式(11)に代入すると次式が得られます。
U=∫∫(T2/2GIP2)r2dAdx=∫0ℓ(T2/2GIP2)dx・∫Ar2dA ーーー(12)
ここで、∫Ar2dA =Ip を式(12)に代入すると次式となります。
U=∫0ℓ(T2/2GIp)dx ---(13)
次に、引張、曲げ、ねじりなどの応力が衝撃的に発生することがあります。これらの場合、ひずみエネルギーを利用すると便利です。例えば、衝撃引張では静かに荷重を加えるときの2倍の伸び及び応力が発生するので注意が必要です。
ひずみエネルギーに関する二つの定理(数式省略)を紹介(引用:材料力学(黒木))します。
1)カスティリアノ定理(Castigliano's theorem)
多くの荷重によって弾性体に保有されるひずみエネルギーをある荷重で偏微分すると、その荷重の作用点でその荷
重の方向に生ずる変位が与えられる。
2)マックスウェルの定理(Maxwell's theorem)
例えば、A1にP1=1Nだけを作用するときのP2の作用点A2に生ずるP2方向の変位は、A2にP2=1Nだけを
作用するときのP1の作用点A1に生ずるP1方向の変位に等しい。
技術情報メモ38~44において材料力学の基礎知識のいくつかを紹介しました。これら以外にも材料力学では多くの問題を取り扱っています。例えば、JSMEテキストシリーズ材料力学には、「はりの複雑な問題」、「柱の座屈」、「複雑な応力」、「骨組構造とシュミレーション」、「強度と設計」などが、詳述されています。
当事務所では人間行動に起因する事故・品質トラブルの未然防止をお手伝いします。また、ものづくりの現場の皆様の声を真摯に受け止め、ものづくりの現場における労働安全の構築と品質の作り込みをサポートします。 (2013.10.3)
バナースペース
阿部技術士・
労働安全コンサルタント事務所
〒771-1330
徳島県板野郡上板町西分字橋北
16番地2
TEL 088-694-3482
FAX 088-694-3482